Danas
ćemo malo praktičnije... Što je to uzorak, što je populacija i kakve veze jedno
ima s drugim? Recimo da bismo to trebali danas naučiti kroz praktične
primjere...
Najjednostavnije
rečeno... zanima nas rezultat populacije (a ne uzorka) a jedini način
da ga doznamo je iz uzorka! Ponovite ovo 100 puta, 1000 puta ako treba,
rezultat uzorka je apsolutno nezanimljiv sam po sebi,
ne
zanima nas ništa o uzorku a sve o populaciji!
Prema
nekim knjigama uzorci se dijele na one koji se temelje na vjerojatnosti i
"one druge" (kao loše). Čitajte Fielda kao uvod u uvod u uvod u
statistiku (Andy Field: Discovering Statistics using SPSS, ili Discovering...
using R, ili Adventure in Statistics... sve što ja govorim on kaže
još ljepše i bolje, jedino što piše na engleski pa ako vam se ne da čitat
engleski onda ste zapeli tu na Fieldu za sirotinju ako se smijem tako nazvati
za malo kasnije od uvoda imate Miles i Shevlin: Applying regression and
correlation a dalje ćete već i sami naći što je i gdje dobro).
Znate
ono kad su izbori ili netko nešto istražuje pa kaže uz granicu pogreške (ili
tako nešto kažu televzijski voditelji)?
TV
voditelj: "Prema anketi koju smo
naručili od neke agencije ovo su njihova predviđanja rezultata izbora, Milanović
vodi s 20% glasova, slijedi ga Grabar-Kitarović s 18% i treći kandidat je Škoro
s 15% glasova. Istraživanje je provedeno na uzorku od 14000 glasača. Pritom je
važno napomenuti da statistička pogreška iznosi +/- 2,5%."
Voditelj iz studija: "Kolega, za gledatelje koji nisu
upoznati s ovim pojmovima, što bi značila statistička pogreška od +/- 2,5 %?
Znači li to možda da su pogriješili za 2,5% ili da će u 97,5% puta biti u pravu
prognozirajući rezultate? Moramo priznati, konfuzija vlada u studiju i režiji..."
TV
Voditelj: "..."
Voditelj
iz studija: "..."
Promidžbeni
program...
E pa
da ne biste tumarali svijetom ne znajući što se tu zbiva možda vam ja uspijem
prenijeti djelić atmosfere onoga što se zbiva. Putovat ćemo kroz vrijeme (iz
potpuno krivih razloga). Vratit ćemo se u prošlost kako bismo ispitali ljude za
koga će glasati (inače bismo putovali natrag u vrijeme sa znanjem tko će
pobjediti pa bismo se kladili na njega i lijepo zaradili, ali kao što je
uobičajeno, u obrazovanju nisu neki novci pa idemo na put, i vraćamo se,
praznih džepova).
Zahvaljujući
novim tehnologijama, na stranici izbora
imate mogućnost pregleda rezultata koje smo dali kojem predsjedničkom kandidatu
u prvom krugu. Ja sam te podatke pretvorio u glasove ljudi. Ne
zaboravite: ovo je populacija koju nikad ne znamo (ili ne znamo
na vrijeme, šta nam sad vrijedi znati tko je prošao u drugi krug.. ništa) ali
korisno je za pokazati važnost uzorka i reprezentativnosti uzorka...
Kako
ne bismo varali, pravit ćemo se (za sad) da nemamo uvid u to kako će populacija
glasovati već ćemo igrati pošteno te obzirom na uzorak pokušati predvidjeti
pobjednika prvog kruga izbora. U tu svrhu odabrali smo 100 ljudi (nekako ljudi
misle da je 100 mnogo, pa neka bude za prvu.. imajte na umu da je u ovom
slučaju to 0.003% populacije, ali OK negdje moramo krenuti..) i dobili smo
sljedeće (pazite ovo je pod pretpostavkom da smo imali savršeni slučajni
uzorak - svaki pripadnik populacije je imao jednaku vjerojatnost biti
izabran u uzorak - nešto što u praksi nikad ili skoro pa nikad [al zapravo
stvarno nikad] nećete imati):
Iz
rezultata analize odgovora ovog uzorka zaključili bismo da će u idući krug
Milanović i Škoro. Recimo da je jedna TV kuća uzela drugu agenciju za
istraživanje tržišta koji su na uzorku jednake veličine (N = 100 što bi naš
voditelj s početka priče rekao) i pronašli su sljedeće:
Prema
njima u drugi krug sigurno ide Miroslav Škoro a na zajedničkom drugom mjestu nalaze se Kolinda Grabar Kitarović i Zoran Milanović. Novinska kuća platila
je svoju agenciju, susjedna TV kuća svoju, Amerikanci (koje odjednom počelo
zanimati tko će pobijediti na hrvatskim predsjedničkim izborima) svoju itd. I
što se dogodi? Kandidati napadaju ankete kako one nisu točne ni istinite jer
lažno pozivaju birače na glasanje i kojezna kakve još nebuloze, agencije se
kunu u njihovu točnost (do objave službenih rezultata, onda se okreću
statističkoj pogrešci itd).
Pazite, ova dva uzorka koja sam ja imao su savršena! Pod savršena mislim sljedeće:
-
oba su savršeni slučajni uzorci u kojima je svaki ispitanik kojega je
kocka dopala zaista i odgovorio na postavljeno pitanje za koga će glasati
-
oba su savršeno točna u smislu da svaki ispitanik iz oba uzorka je na kraju
zaista i glasao za kandidata za kojega je i rekao da će glasati (nije ga
žena nagovorila da podrži njenu kandidatkinju ;)
-
predstavljaju cijelu Hrvatsku ravnomjerno, neki iz uzorka su možda
svjetioničari bez mobitela i televizije ali su mi svejedno odgovorili na
pitanje za koga će glasati...
-
Ovo sve govorim da naglasim kako će stvarni uzorci biti puno gori nego ovi (koji
prognoziraju Škoru u drugom krugu)
Kako
to da jedan prognozira jedan ishod a drugi prognozira drugi ishod??? Šlag na
tortu je da su oba savršeno točna (onoliko koliko mogu biti točna!).
Dakle,
ovo je najjednostavniji slučaj na kojem ćemo pričati o pogrešci mjerenja. Ali,
ona će biti s nama u sve dane života našega. Iako pogreška mjerenja uvijek
ovisi o veličini uzorka, ovdje ovisi isključivo o veličini uzorka (vidjet ćete
kasnije kada imamo intervalne varijable kojima računamo aritmetičku i
standardnu da ovisi i o varijabilitetu al o tom-po tom). Ja sam pogrešku
mjerenja (obzirom na veličinu uzorka od 100 i veličinu populacije od 3719141)
izračunao ovdje. Moramo unesti veličinu populacije,
veličinu uzorka i interval pouzdanosti. Ajmo na sekundu preskočiti
interval pouzdanosti, objasnit ćemo ga poslije, zasad samo stavite 95 (ako
morate nešto staviti već). Pazite, ovu pogrešku računamo samo ako nam je cilj
istraživanja brojati nominalne odgovore (dakle, ako nas zanima koliki je udio
muškaraca i žena u populaciji, ako nas zanima koje je ime češće Matia ili
Vatroslav, ako nas zanima posjećuju li potrošači Konzum ili Plodine itd...;
ovaj kalkulator nećemo koristiti ako nas zanima tko je viši muškarci ili
žene, nećemo ga koristiti ako nas zanima koji proizvod kupci više
preferiraju itd.). Ovo je obična formula s jednom nepoznanicom - ne znamo
koliko pogrešku mjerenja radimo u slučaju kada imamo uzorak veličine n i
populaciju veličine N. Ali! nitko nam ne brani, dapače, neki nam naređuju (Laakens na svom blogu, čitajte i njega, on to
puno ljepše objasni, ali zahtjeva maaalo naprednije znanje osnovnih pojmova) da
unaprijed odredimo s koliko granicom greške bismo bili zadovoljni (odnosno
kolika bi bila dovoljna da razlikujemo dvije grupe).
Pa
npr. ako nas zanima kupuju li Hrvati više Mercedese ili BMW-e možemo potražiti
omjere Mercedes i BMW u našim susjednim zemljama da otprilike znamo koliko su
blizu jedni od drugih, pa ako npr. u Sloveniji imamo 34% ljudi koji imaju
Mercedes a 10% ljudi koji imaju BMW. Razlika je 24% pa si možemo priuštiti i
granicu pogreške od npr. 10% (to bi značilo da Mercedes ima između 24% i 44% a
BMW ima između 0% i 20% ljudi) jer bismo uspjeli ustanoviti kojih automobila
ima više (dakle ti intervali se ne bi smjeli poklapati - idealno; ili barem ne
bi smjeli sadržavati opaženi rezultat druge grupe unutar njih). Ovo je bitno
jer veći uzorak = manja granica greške i obrnuto.
Ako npr. želimo prognozirati ishod predsjedničkih izbora možemo se okrenuti nazad u vrijeme i vidjeti kolike su razlike presuđivale u dosadašnjim izborima (recimo da je najmanja razlika među kandidatima bila 4%, možda je netko imao 48% a pobjednik 52%) i onda odaberemo prihvatljivu razinu pogreške tako da nam se ne dogodi da bude preveliko preklapanje, u ovom slučaju bismo se odlučili na granicu greške od 2% što bi značilo da će za jednog kandidata glasati između 46-50% ljudi a za drugog 50-54% ljudi - dakle bitno nam je da se ta dva intervala ne preklapaju! (u slučaju predsjedničkih izbora u drugom krugu trebalo bi nam 3000 ispitanika kako bismo tu granicu pogreške sveli na razinu 2%).
Sad malo o intervalu pouzdanosti... Ako smo prognozirali da će Milanović ući u 2. krug s rezultatom od 18% uz granicu pogreške od 2% na uzorku od 3000 ljudi to znači sljedeće:
Kad
bismo ponovili istraživanje 100 puta na uzorku jednake veličine (to nitko nikad neće napraviti ali zamislimo da je 100 puta
proveo istraživanje na različitim uzorcima od 3000 ljudi), u 95 uzoraka će
opaženi rezultat (možda u jednom uzorku 17% ljudi kaže da će glasat za
Milanovića, u drugom 17,5, u trećem 20%...) se nalaziti između 18+/-2%...
Pogledajmo
sljedeću sliku koja prikazuje prave rezultate (prvi, rozi stupac kod svakog
kandidata i predviđanja temeljena na rezultatima anketiranja pet uzoraka od 100
ljudi):
Što
opažate? Pa i ne baš puno jer je malo nejasan graf.. Na sljedećoj slici sam
ubližio foto-finiš (na kraju krajeva samo to je i bitno) tri kandidata s
najvećim brojem glasova:
Kao
što sam rekao, prvi stupac kod svakog kandidata je stvarni njihov rezultat, tj.
ono šti se na kraju dogodilo... Ali, pogledajte rezultate različitih uzoraka...
npr. u Uzorku 1 (smeđa boja) Škoro i Grabar Kitarović su imali jednak broj
glasova a Milanović je bio 3., u Uzorku 2 npr. Škoro je išao u drugi
krug umjesto KGK itd. Sjećate se da sam rekao da su uzorci savršeni i
savršeno točni (obzirom na njihovu veličinu), na sljedećoj slici je identičan
graf na koji sam dodao interval pouzdanosti odnosno granicu greške (koji za 100 ljudi od ukupno 3,7
milijuna iznosi +/-10%):
Nekoliko
je stvari očito (iskusnom oku, a nešto manje mom) na prethodnom grafu:
-
kao prvo, svjesni smo da 100 zapravo i nije nešto prevelik uzorak... Ako
pogledate ove granice greške (ogromne su...), svi kandidati u svim uzorcima su
u svim intervalima.. Dakle ne možemo reći (na temelju ovog grafa) ne tko će
pobijediti već ni tko će ići u drugi krug...
-
Drugo što primjećuje (i manje iskusno oko) je da oko rezultata u
populaciji nema granice greške.. Naravno da nema jer je to ono što želimo znati
(to je jedna jedina vrijednost) a nikad (u pravom svijetu) ne znamo...
-
Treće što je vidljivo je da kad pogledate svakog kandidata posebno...
njegova/njezina zvjezdica se nalazi unutar svakog intervala od svih 5 uzoraka (gledajte
sad samo 6 Milanovićevih stupaca, ili samo 6 Škorinih ili samo 6 Kolindinih,
svejedno je)... Dakle tih 5 uzoraka su jedni od onih 95 kod kojih će
taj "stvarni" rezultat iz populacije biti unutar tih intervala pouzdanosti..
Da sam uzorkovao 20 puta, vrlo vjerojatno bi se dogodio jedan uzorak (5%) u kojem se rezultat u populaciji ne bi nalazio unutar tog intervala
pouzdanosti...
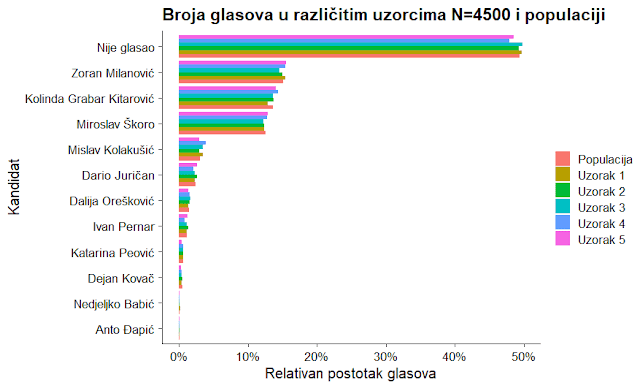
Za
kraj, ponovimo sve ali sad sam uzorkovao 4500 ljudi u svakom uzorku (prema
onoj stranici koju sam linkao gore, 4500 ljudi je dovoljno da granicu pogreške
smanjimo na +/-1%):
Kako
to lijepo sad izgleda, više manje koji god uzorak gledali, predvidjet ćemo
isto:
a) da
Milanović i KGK idu u drugi krug (u svakom uzorku je isti rezultat).
b)
unutar svakog kandidata njegov konačni rezultat spada unutar granice
pogreške svakog uzorka.
c)
Iako ne vidim precizno (moj grijeh, dosta mi je malo ovih grafova za neko
vrijeme...) ali mi se čini da se procjene broja glasova svakog kandidata unutar
istog uzorka ne nalaze unutar granice pogreške ostalih kandidata (ako se
sjećate to znači da postoji statistički značajna razlika - dobro
zapamtite ovu frazu... i ona će biti s nama u sve dane života našega).
d)
veće je uvijek bolje, pa tako i s uzorcima. Naći ćete različite cut-off
vrijednosti i opravdanja (5-10 puta broj varijabli koje imate, više od 100, bla
bla) o tome koliko ispitanika je dovoljno. Jedino što je bitno za unaprijed
odrediti broj ispitanika je veličina efekta kojeg istražujemo (u slučaju našeg
primjera s autima je to procjena razlike između postotka ljudi koji voze
Mercedes ili BMW npr.).
Da je
samo zadnja rečenica ostala u glavi - ja zadovoljan.
Stvarno
ne znam šta je sljedeći put na repertoaru, ali znam da nije korelacija... još
uvijek.
***Mali
disclaimer, izbori se odlučuju obzirom na relativan broj glasova (dakle na
većinu birača koji su izašli na izbore a ne na ukupan broj ljudi koji imaju
pravo glasa) ali kad sam već imao priliku vidjeti cijelu cijelcatu populaciju
bila mi je šteta to ne i napraviti, dakle ovaj rezultat da je Zoki imao 16-ak%
glasova se odnosi na 16% glasova od svih ljudi koji su imali pravo glasa a ne
od svih ljudi koji su glasali.. isti vrag bi bio da sam kao populaciju uzeo
samo ljude koji su glasali pa nisam ništa mijenjao.. srž ostaje ista al evo,
samo da naglasim***
Lp,
Matia








Nema komentara:
Objavi komentar